アカデミーアドベンチャー攻略その１２（ネタバレ注意）

＜注意＞
　本記事は筆者がプレイした限りで収集した情報を元に記述しています。そのため、情報に誤りがあったり、アップデートによって変更が加えられる可能性があります。この情報を元にプレイした結果、予想外の結末となっても一切責任は持てませんのでご了承下さい。
　勿論、誤りの指摘や情報の追加は歓迎致します。

-------------------
シナリオ１４：不届き者を追え

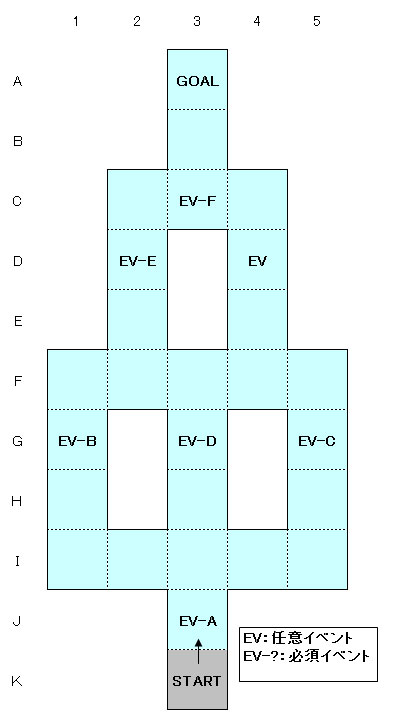
　マップは縦に長いですが、構造自体は比較的シンプルです。また、後述するイベントマスを除き、高ボーダー地帯は無く、全てのマスで150程度と最低レベルのボーダーとなっています。

　本シナリオは☆４とこれまでのシナリオで最高難易度タイですが、畑の害獣退治と同様、イベントが面倒なタイプで、モンスターの討伐自体は難しくありません。また、目的がある程度は明示されているため、害獣退治と違って行き先が分からなくてムダにクレジットを投入する必要が多少は少なくて済んでいます(^_^;。全てのイベントマスを総当たりで行けば何となくでもグッドエンドにはたどり着けるでしょう。

　グッドエンドを迎える具体的な手順は以下の通りになります。

EV-Aでリディア先生と会話する(会話後、マップから消える) 　↓ EV-Bでレオンと会話する(会話してもマップから消えないが、フラグは立つ) 　↓ EV-Cでルキアと会話する(会話してもマップから消えないが、フラグは立つ) 　↓ EV-Dでシャロンと会話する(会話してもマップから消えないが、フラグは立つ) 　↓ ここまでのフラグを全て消化するとEV-EとEVが出現するので、EV-Eで不届き者を発見し、会話する(会話後、マップから消える。EVはハズレなので行く必要は無い。EV-Eを消化するとEVは一緒に消滅する) 　↓ EV-Fが出現するので、EV-Fでクレッセントホーンを討伐する(討伐後、マップから消える) 　↓ ゴールする

　これまでの場合、スタート地点すぐそばにいる先生は単なる解説役であることがほとんどで、エンディング評価に関係しなかったのですが、今回はきっちりフラグを持っていることに注意が必要です。リディア先生と会話していないと他のキャラと会話しても見つけたという話を得られません。幸か不幸か、スタートの隣かつ丁度の数でなくても止まれます（本シナリオのイベントマスは全て丁度でなくても止まれます）ので、手持ちのカードで最小のものを使って会話を済ませてしまいましょう。

　続けてレオン、シャロン、ルキアとの会話ですが、全員と話せば良いわけではなく、特定の順番で話す必要があります。幸い、レオン→ルキア→シャロンの順に話せば間に誰かが挟まっていたり、連続して話してもリセットされるわけではありませんが、リディア→レオンで５マス、レオン→ルキアで６マス、ルキア→シャロンで４マスと大きい数のカードが無いとターン数がかかってしまうのが頭の痛いところです。また、正しい順序で話して「見つけた」という情報を得られてもマップから消えないので、まだ未消化のイベントがあるのか？と混乱しないようにご注意を。
　リディア先生と話さずに生徒キャラと話す、レオンと話さずにシャロン・ルキアと話す、レオン・ルキアと話さずにシャロンと話すなど、必要なフラグを立てていない場合、「見つけていない」という情報しか得られません。

　全ての会話イベントを消化すると、EV-EとEVに「！」のイベントマスが出現します。当たりはEV-Eで、EVのマスに行っても怪しい者はいないというメッセージとガラス玉が落ちているのみです。

　EV-Eのイベントも消化するとEV-Fに「！」のイベントマスが出現します。ここには固定でクレッセントホーンが出現し、問題の難易度上昇・ノルマの増加・問題数が８問に増加と森の均衡などにもあった大型モンスタールールでの戦闘となります。ノルマはおおよそ400台後半で、順調に正解できれば４～５問で倒せるぐらいのようです。クレッセントホーンを討伐すると不届き者との会話イベントが発生し、イベントクリアとなります。あとはそのままゴールすればグッドエンドとなります。

　エンディング分岐ですが、

・クレッセントホーンを討伐した　→　グッドエンド
・クレッセントホーンを出現させたが討伐していない　→　ノーマルエンド
・クレッセントホーンを出現させていない　→　バッドエンド

と思われます（グッド・ノーマルのみ確認。バッドは推測です）。立てなければならないフラグが多く、その間隔も理想のカードがあれば１手で済むものの、そう上手く揃ってはくれないことが多いでしょうから、３クレ必要となる可能性も高いと思われます（最短は１→５→６→４→４→２→２の７手）。